Answer:
W=12 cm, L=18 cm
Explanation:
given:
The length of a rectangle is 6 centimeters less than two times its width.
The area of the rectangle is 216
square centimeters.
find:
What are the dimensions of the rectangle?
solution:
area of a rectangle = Length(L) x Width(W)
where
A = 216 cm²
L = 2W - 6
plugin values into the formula
216 = (2W - 6) W
216 = 2W² - 6W
rearrange:
2W² - 6W - 216 = 0
solve W by using quadratic equation:
- (-6) ±
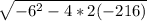
W = -------------------------------------------
2 (2)
W = 12; W = -9
solve L: substitute W=12 into L = 2W - 6
L = 2W - 6
L = 2(12) - 6
L = 18 cm
therefore:
the dimensions of the rectangle is W=12 cm, L=18 cm