Answer:
24.03 units (nearest hundredth)
Explanation:
The distance between B and A is: AB = AH + HB
We have been given AH, so we just need to find the measure of HB.
First, find the angle AOH using tan trig ratio:
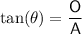
where:
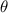 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Given:
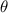 = ∠AOH
= ∠AOH- O = AH = 8
- A = OH = 19.80
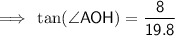
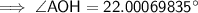
∠BOA = ∠BOH + ∠AOH
⇒ ∠BOH = ∠BOA - ∠AOH
⇒ ∠BOH = 61° - 22.00069835°
= 38.99930165°
Now we can find HB by again using the tan trig ratio:
Given:
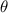 = ∠BOH = 38.99930165°
= ∠BOH = 38.99930165°- O = HB
- A = OH = 19.80
Substituting given values:
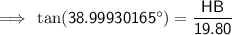
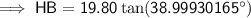
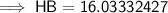
Therefore:
AB = AH + BH
⇒ AB = 8 + 16.03332427
= 24.03 units (nearest hundredth)