Question

F divides HJ in the ratio 3:1. If H = (-11,7) and J = (5,3), what are the
coordinates of F?

Answer 1

The coordinates of HF are (1, 4)

Explanation:

The parameters of the line are;

The coordinate of the end points are H = (-11, 7), and J = (5, 3)

The ratio by which the point F divides the line = 3:1

The segments in the line are HF, and FJ

Therefore;

The fraction of the length of HJ that is represented by HF = 3/(3 + 1) × HJ = 3/4 × HJ

HF = 3/4 × HJ

Which gives the coordinates of the point F as follows;

Coordinate of F = (-11 +(5 - (-11))×3/4, 7 + (3 - 7)×3/4) = (1, 4)

The coordinates of F are (1, 4)

We check the length of HF, from the equation for the length to of a line to get;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

`l_(HF) = \sqrt{\left (4-7 \right )^(2)+\left (1-(-11) \right )^(2)} = \sqrt{\left (-3 \right )^(2)+\left (12 \right )^(2)} = 3\cdot √(17)`

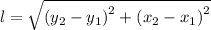
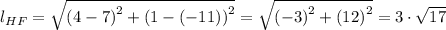
Similarly, we check the length of HJ, to get;

`l_(HF) = \sqrt{\left (3-7 \right )^(2)+\left (5-(-11) \right )^(2)} = \sqrt{\left (-4 \right )^(2)+\left (16 \right )^(2)} = 4\cdot √(17)`

The length of HF = 3·√(17)

The length of HJ = 4·√(17)

Therefore, from HF = 3/4× HJ, we have;

HF = 3/4 × 4·√(17) = 3·√(17)

Therefore, the coordinates of HF are (1, 4)