Answer:
Explanation:
From the given information:
The null hypothesis and the alternative hypothesis can be computed as:
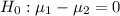 (i.e. there is no difference between the SAT score for students in both locations)
(i.e. there is no difference between the SAT score for students in both locations)
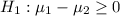 (i.e. there is a difference between the SAT score for students in both locations)
(i.e. there is a difference between the SAT score for students in both locations)
The test statistics using the students' t-test for the two-samples; we have:
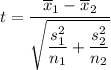
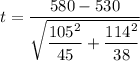

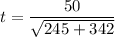
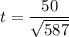
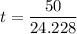
t = 2.06
degree of freedom = (
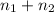 ) -2
) -2
degree of freedom = (45+38) -2
degree of freedom = 81
Using the level of significance of 0.05
Since the test is two-tailed at the degree of freedom 81 and t = 2.06
The p-value = 0.0426
Decision rule: To reject
 if the p-value is less than the significance level
if the p-value is less than the significance level
Conclusion: We reject the
 , thus, there is no sufficient evidence to conclude that there is a significant difference between the SAT math score for students in Pennsylvania and Ohio.
, thus, there is no sufficient evidence to conclude that there is a significant difference between the SAT math score for students in Pennsylvania and Ohio.