Question

A toy rocket is launched with an initial velocity of 10.0 m/s in the horizontal direction from the roof of a 30.0 m -tall building. The rocket's engine produces a horizontal acceleration of (1.60 m/s3)t, in the same direction as the initial velocity, but in the vertical direction the acceleration is g , downward. Air resistance can be neglected.

What horizontal distance does the rocket travel before reaching the ground?

Answer 1

The toy rocket will do an horizontal distance of 27.793 meters before reaching the ground.

Step-by-step explanation:

This rocket experiments a two-dimension motion consisting in a combination of vertical free-fall and a horizontal uniformly acclerated motion. Flight time is governed by vertical movement and can be found by using this formula:

`y = y_(o)+v_(o,y)\cdot t +(1)/(2)\cdot g \cdot t^(2)`

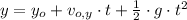
Where:

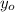`y_(o)` - Initial height, measured in meters.

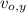`v_(o,y)` - Initial vertical speed, measured in meters per second.

`t` - Time, measured in seconds.

`g` - Gravitational acceleration, measured in meters per square second.

`y` - Current height, measured in meters.

If we know that
`y_(o) = 30\,m`,
`v_(o,y) = 0\,(m)/(s)`,
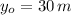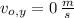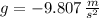`g = -9.807\,(m)/(s^(2))` and
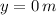`y = 0\,m`, then resulting polynomial is solved:

`0\,m = 30\,m +\left(0\,(m)/(s) \right)\cdot t +(1)/(2) \cdot \left(-9.807\,(m)/(s^(2)) \right)\cdot t^(2)`

`30 - 4.905\cdot t^(2) = 0`

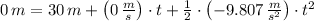
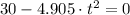
The time taken by the toy rocket is:

`t \approx 2.407\,s`

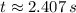
Now, the horizontal distance can be found by integrating acceleration function twice. That is:

`v(t) = \int {a(t)} \, dt`

`v(t) = 1.60\int {t} \, dt`

`v(t) = 0.80\cdot t^(2)+v_(o)`

`s(t) = \int {v(t)} \, dt`

`s(t) = \int {(0.80\cdot t^(2)+v_(o))} \, dt`

`s(t) = 0.80\int {t^(2)} \, dt + v_(o)\int\, dt`

`s(t) = 0.267\cdot t^(3) + v_(o)\cdot t + s_(o)`

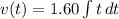
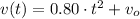
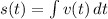
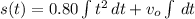
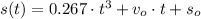
If we know that
`v_(o) = 10\,(m)/(s)` and
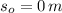`s_(o) = 0\,m`, then the horizontal position formula is:

`s(t) = 0.267\cdot t^(3)+10\cdot t`

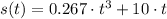
Where:

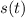`s(t)` - Horizontal position, measured in meters.

`t` - Time, measured in seconds.

Now, the horizontal distance before reaching the ground is found: (
`t \approx 2.407\,s`)

`s(2.407\,s) = 0.267\cdot (2.407\,s)^(3)+10\cdot (2.407\,s)`

`s (2.407\,s) = 27.793\,m`

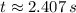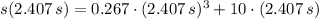
The toy rocket will do an horizontal distance of 27.793 meters before reaching the ground.