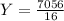Question

The square of X varies inversely as the square root of Y and directly as the variable M. When M = 27 and Y = 16, then X = 9. Find the exact value of Y when M = 7 and X = 2

Answer 1

`Y = 441`

Explanation:

Given

M = 27 when Y = 16 and X = 9

Required

Find Y when M = 7 and X = 2

We start by getting the algebraic representation of the given statement

`X^2 \alpha (1)/(\sqrt Y) \alpha M`

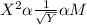
Convert the variation to an equation; we have

`X^2 = (KM)/(\sqrt Y)`

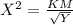
Where K is the constant of variation;

When M = 27; Y = 16; X = 9, the expression becomes

`9^2 = (K * 27)/(√(16))`

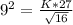
This gives

`81 = (k * 27)/(4)`

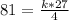
Make K the subject of formula

`K = (81* 4)/(27)`

`K = (324)/(27)`

`K = 12`

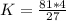
Solving for Y when M = 7 and X = 2

Recall that
`X^2 = (KM)/(\sqrt Y)`

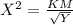
Substitute values for K, M and X

`2^2 = (12 * 7)/(√(Y))`

`4 = (84)/(√(Y))`

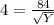
Take square of both sides

`4^2 = ((84)/(√(Y)))^2`

`16 = (7056)/(Y)`

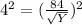
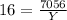
Make Y the subject of formula

`Y = (7056)/(16)`

`Y = 441`