Question

Suppose a quiz contains 20 true/false questions. You know the correct answer to the first 10 questions. You have no idea of the correct answer to questions 11 through 20 and decide to answer each using the coin toss method. Calculate the probability of obtaining a total quiz score of at least 85%

Answer 1

0.1719

Explanation:

Given that:

A quiz contains 20 questions and 10 questions have been answered rightly

We are to determine the probability of getting a total quiz score of 85%

i.e 0.85 (20) = 17

Let's not forget that 10 is correctly answered out of 17. that implies that we only have 7 more questions to make a decision on.

where;

n = 10,

p + q = 1, 0.5 + q = 1

q = 1 - 0.5

q = 0.5

Let X be the random variable that follows the binomial distribution. Then ;

`P(X = x) =(^n_x) p^x q^(n -x)`

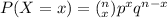
where x = 7

`P(X \geq 7) =P(X=7)+P(X=8)+P(X=9)+P(X=10)`

`P(X \geq 7) =(^(10)_7})\ 0.5^7 \ 0.5 ^(10-7) + (^(10)_(8))\ 0.5^8 \ 0.5 ^(10-8)+(^(10)_9})\ 0.5^9 \ 0.5 ^(10-9)+ (^(10)_(10)})\ 0.5^(10) \ 0.5 ^(10-10)`

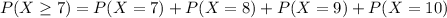
P(X ≥ 7) = 0.1719