Question

Consider the differential equation (x - 1)y" + y' = 0. By using power series so- lution about the ordinary point 0 we obtain: c_{k+1)=[(k+1)/(k+2)] C_(K); k=1,2,3.... c_(K+2)=[(k+1)/(k+2)] C_(K+1); k=0,1,2,3... None of them c_(k+2)=[(k+1)/(k+2)] C_(k+1); k=1,2,3....​

Answer 1

Given the ODE

(x - 1) y'' + y' = 0

we assume a solution of the form

`y(x) = \displaystyle \sum_(n=0)^\infty c_n x^n`

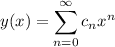
with derivatives

`y'(x) = \displaystyle \sum_(n=0)^\infty n c_n x^(n-1) = \sum_(n=0)^\infty (n+1) c_(n+1) x^n`

`y''(x) = \displaystyle \sum_(n=0)^\infty (n+1) n c_(n+1) x^(n-1) = \sum_(n=0)^\infty (n+2)(n+1) c_(n+2) x^n`

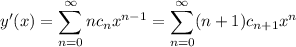
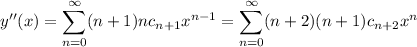
Substituting these series into ODE gives

`\displaystyle (x - 1) \sum_(n=0)^\infty (n+2)(n+1) c_(n+2) x^n + \sum_(n=0)^\infty (n+1) c_(n+1) x^n = 0`

`\displaystyle \sum_(n=0)^\infty (n+2)(n+1) c_(n+2) x^(n+1) - \sum_(n=0)^\infty (n+2)(n+1) c_(n+2) x^n + \sum_(n=0)^\infty (n+1) c_(n+1) x^n = 0`

`\displaystyle \sum_(n=1)^\infty (n+1)n c_(n+1) x^n - \sum_(n=0)^\infty (n+2)(n+1) c_(n+2) x^n + \sum_(n=0)^\infty (n+1) c_(n+1) x^n = 0`

`\displaystyle \sum_(n=1)^\infty \bigg((n+1)n c_(n+1) - (n+2)(n+1) c_(n+2) + (n+1) c_(n+1)\bigg) x^n - 2c_2 + c_1 = 0`

`\displaystyle \sum_(n=1)^\infty \bigg((n+1)^2 c_(n+1) - (n+2)(n+1) c_(n+2)\bigg) x^n - 2c_2 + c_1 = 0`

`\displaystyle \sum_(n=0)^\infty \bigg((n+1)^2 c_(n+1) - (n+2)(n+1) c_(n+2)\bigg) x^n = 0`

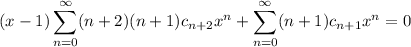
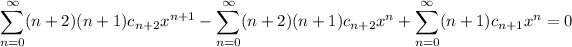
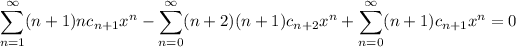
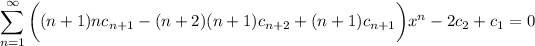
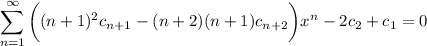
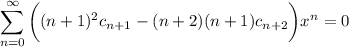
Then the coefficients
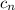`c_n` are given recursively by

`(n+1)^2 c_(n+1) - (n+2)(n+1) c_(n+2) = 0`

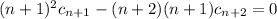
for all n ≥ 0, or equivalently,

`c_(n+2) = (n+1)/(n+2) c_(n+1)`

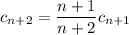
which most closely resembles the second choice.