Complete question
The complete question is shown on the first uploaded image
Answer:
The function is

The domain is [1, 7]
Explanation:
Generally from the Graph we can see that
For the y-coordinate the point of symmetry is
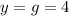
For the x-coordinate the point of symmetry is x = 4
The general form of quadratic equation representing this type of curve is

Now considering the coordinate (4, 3.5) along the axis of symmetry we have that
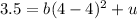
=>

Now considering point B having the coordinates (7,4)
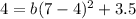


Generally the function that define the given graph is

From the graph the first element for x is 1 (i.e [1 . 4] )and the last element for x is 7 (i.e [7,4])
So the domain of the function is [1, 7]