Question

How do I factor x^4-5x^2+6?

Answer 1

`=(x^2-3)(x^2-2)`

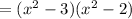
Explanation:

So we have the expression:

`x^4-5x^2+6`

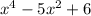
And we wish to factor it.

First, let's make a substitution. Let's let u be equal to x². Therefore, our expression is now:

`=u^2-5u+6`

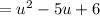
This is a technique called quadratic u-substitution. Now, we can factor in this form.

We can use the numbers -3 and -2. So:

`=u^2-2u-3u+6`

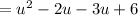
For the first two terms, factor out a u.

For the last two terms, factor out a -3. So:

`=u(u-2)-3(u-2)`

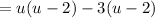
Grouping:

`=(u-3)(u-2)`

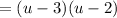
Now, substitute back the x² for u:

`=(x^2-3)(x^2-2)`

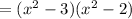
And this is the simplest form.

And we're done!