Question

(a) (4 3 , 4)

(i) Find polar coordinates (r, θ) of the point, where r > 0 and 0 ≤ θ < 2π. (r, θ) =
(ii) Find polar coordinates (r, θ) of the point, where r < 0 and 0 ≤ θ < 2π. (r, θ) =
(b) (1, −3)
(i) Find polar coordinates (r, θ) of the point, where r > 0 and 0 ≤ θ < 2π. (r, θ) =
(ii) Find polar coordinates (r, θ) of the point, where r < 0 and 0 ≤ θ < 2π. (r, θ) =

Answer 1

The answer is below

Explanation:

A point in the coordinate plane can either be represented using the Cartesian form or the polar corm. The Cartesian form is represented as (x, y) where x and y are the horizontal and vertical coordinates while the polar form is represented as (r, θ), θ is the angle and r is the length.

Conversion of (x, y) to (r, θ) is:

`r=√(x^2+y^2)\\ \\\theta=tan^(-1)((y)/(x) )`

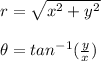
a) (3, 4)

`r=√(3^2+4^2)=5\\ \\\theta=tan^(-1)(4)/(3)=53.13^o=0.295\pi`

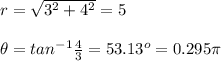
(3, 4) = (5, 0.296π)

b) (1, -3)

`r=√(1^2+(-3)^2)=√(10) \\ \\\theta=tan^(-1)(-3)/(1)=1.6\pi`

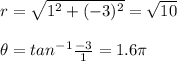
(3, 4) = (√10, 1.6π)