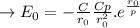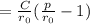Answer:
The following are the solution to this question:
Step-by-step explanation:
Total energy capacity EN from adjacent ions is:
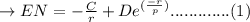
where the value of "C, D, and "r is constants.
In point a:
Differentiating EN:
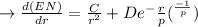
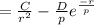
In point b:
The above equation is equal to zero to get the value of C:
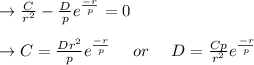
The
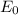 value is replaced by the C value in (1):
value is replaced by the C value in (1):
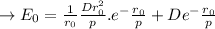
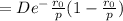
The
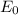 value is replaced by the D value in (1):
value is replaced by the D value in (1):