Question

You climb to the top of a 50.0m cliff, hold your hand out over the edge, and toss a rock straight up into the air with a velocity of 20.0m/s. Find (a) the time it takes the rock to reach maximum height, (b) the maximum height, (c) the time it takes the rock to reach the ground, (d) the velocity of the rock as it hits the ground.

Answer 1

Step-by-step explanation:

Given that,

Initial position, h₀ = 50 m

A rock is tossed straight up into the air with a velocity of 20.0m/s

(a) When the rock reaches its maximum height, its final velocity, v = 0. Using equation of kinematics as follows :

v=u+at

here, a = -g

`t=(u)/(g)\\\\t=(20\ m/s)/(10\ m/s^2)\\\\t=2\ s`

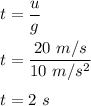
(b) Let h is the maximum height reached by the toss. It can be given by :

`h=h_0+ut-(1)/(2)gt^2\\\\h=50+20* 2-(1)/(2)* 10* 2^2\\\\h=70\ m`

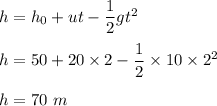
(c) Let T is the time it takes the rock to reach the ground. It is equal to the sum of time reaches to its maximum height and the remaining time. It can be calculated as follows :

`T=t+\sqrt{(2h)/(g)}`

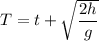
Putting all the values,

`T=2+\sqrt{(2* 70)/(10)}\\\\T=5.74\ s`

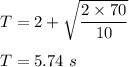
(d) Let v is the velocity of the rock as it hits the ground. It can be calculated as follows :

v = u - gt

`v = 20 - (10)(5.74)\\\\v=-37.4\ m/s`

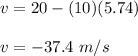
Negative sign shows it comes in downward direction.