Question

A ship sets out to sail to a point 116 km due north. An unexpected storm blows the ship to a point 121 km due east of its starting point. (a) How far (in km) and (b) in what direction (as an angle from due east, where north of east is a positive angle) must it now sail to reach its original destination?

Answer 1

Step-by-step explanation:

In this problem, we are meant to slove for the resultant and the direction of the the vectors given

Given data

let the sail to a point due north be y= 116km

and the point due east be x= 121 km

(a) How far (in km)

The resultant between the two points is the distance between them

`r=√(x^2+y^2) \\\\r=√(121^2+116^2) \\\\r=√(14641+13456) \\\\r=√(28097) \\\\r=167.62`

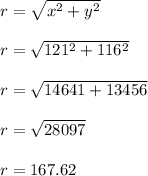
The distance between the points is 167.62

(b) in what direction (as an angle from due east, where north of east is a positive angle) must it now sail to reach its original destination

the direction can be gotten using

tan∅= y/x

∅= tan-1 (y/x)

∅= tan-1(116/121)

∅= tan-1(0.958)

∅= 43.77°

The direction is 43.77°