Question

SOLVING QUADRATIC EQUATIONS
2) Solve 2x2 - 5 = 27

Answer 1

`\boxed{ \bf \huge \: x =4}`

`\rm \: Or,`

`\boxed{\bf \huge \: x = - 4}`

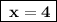
Step by step explanation:

Given Equation is :-

`\sf \implies \: 2 {x}^(2) - 5 = 27`

We need to find the value of
`x` using Quadric formula.

Firstly, Subtract 27 from both of the side(s):-

`\sf \implies2 {x}^(2) - 5 - 27 = 27 - 27`

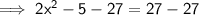
On Simplification:-

Add -5-27 as (-) and (-) equals to (+). -5-27 would be represented as 5+27, which results to 32.

`\sf\sf \implies2 {x}^(2) - 32 = 0`

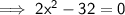
Then, for this equation , a=2, b=0, c=-32.

Put the values :-

That is,

`\sf \implies2 {x}^(2) + 0x + ( - 32) = 0`

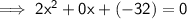
As we know, that the quadratic formula is:-

`\sf \implies \: x = \frac{ -b \pm \sqrt{b {}^(2) - 4ac } }{2a}`

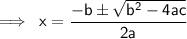
Put the values :-

`\sf \implies \: x = \frac{ - 0 \pm \sqrt{0 {}^(2) \: - 4(2) ( - 32)} }{2(2)}`

On Simplification:-

`\sf \implies \: x = \frac{ - 0 {}^{} \pm \sqrt{ {0 } - \: 8 * - 32}}{2 * 2}`

`\sf \implies \: x = ( - 0 \pm \: √( - 8 * - 32) )/(4)`

`\sf \implies x = \frac{ - {0}^{}\pm \: √( + 256) }{4}`

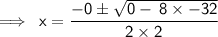
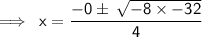
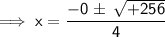
As 0 has no value here,

`\sf \implies \: x = ( \pm √(256) )/(4)`

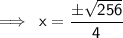
On cancelling,

Remove the square of 256 ( √256)

`\sf \implies \: x = \frac{ \pm \cancel{ \: 256}}{ \cancel4}`

`\sf \implies \: x = ± + 4`

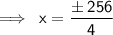
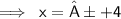
It may be represented as,

`\sf \implies \: x = - 4`

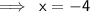
Or,

`\sf \implies \: x = 4`

_______________________________

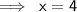
I hope this helps!

Please let me know if you have any questions.

~MisterBrian

Answer 2

x = ±4

Explanation:

Step 1: Write out quadratic

2x² - 5 = 27

Step 2: Add 5 to both sides

2x² = 32

Step 3: Divide both sides by 2

x² = 16

Step 4: Take the square root of both sides

x = ±4

∴ x can equal -4 or 4