Answer:
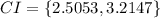
Explanation:
Assuming the conditions for constructing a t-confidence interval are true, we use the formula
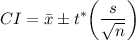 where our sample mean is
where our sample mean is
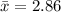 , our sample standard deviation is
, our sample standard deviation is
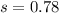 , our sample size is
, our sample size is
 , and a 90% confidence level is equivalent to a critical value of
, and a 90% confidence level is equivalent to a critical value of
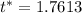 ,
,
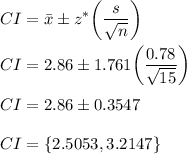
Hence, we are 90% confident that the true population mean of a student's grade point average is between 2.5053 and 3.2147