Question

Solve for the system of equations x/3+2/3=y/6 x/12-y/4=3/2 I need help asap Thank you :)

Answer 1

x = - 6 ; y = - 8

Step-by-step explanation:

In the first linear eqn. in 2 variable ,

`(x)/(3) + (2)/(3) = (y)/(6)`

Simplifying the above eqn. gives =

`(x + 2)/(3) = (y)/(6)`

`= > x + 2 = (y)/(2) ..............(1)`

From eqn.1 value of x in terms of y =

`x = (y)/(2) - 2 = (y - 4)/(2)`

Now in the second linear eqn. in 2 variable ,

`(x)/(12) - (y)/(4) = (3)/(2)`

Simplifying the above eqn. gives =

`(x - 3y)/(12) = (3)/(2)`

`= > x - 3y = (3)/(2) * 12 = 18......(2)`

Substituting the value of x in eqn.2 gives

`(y - 4)/(2) - 3y = 18`

`= > (y - 4 - 6y)/(2) = 18`

`= > ( - 5y - 4)/(2) = 18`

`= > - 5y - 4 = 18 * 2 = 36`

`= > - 5y = 36 + 4 = 40`

`= > y = (40)/( - 5) = - 8`

Putting the value of y in eqn.1 gives =

`x + 2 = ( - 8)/(2) = - 4`

`= > x = - 4 - 2 = - 6`

Answer 2

Answer: The ordered pair (-6, -8)

This means x = -6 and y = -8 pair up together

=============================================================

Step-by-step explanation:

x/3+2/3=y/6 is equivalent to 2x+4 = y after multiplying both sides by the LCD 6. Multiplying both sides by the LCD always clears out the fractions.

Do a similar operation to x/12-y/4 = 3/2 to get x-3y = 18. The LCD in that case is 12.

The original system

`\begin{cases}(x)/(3)+(2)/(3) = (y)/(6)\\\\(x)/(12)-(y)/(4) = (3)/(2)\end{cases}`

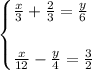
turns into

`\begin{cases}2x+4 = y\\x-3y = 18\end{cases}`

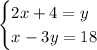
after clearing out the fractions. From here, we can use substitution to solve this equivalent system. The first equation 2x+4 = y is the same as y = 2x+4. We can replace every copy of 'y' in the second equation and solve for x like so...

x - 3y = 18

x - 3( y ) = 18

x - 3( 2x+4 ) = 18 ... y replaced with 2x+4

x - 3(2x) - 3(4) = 18

x - 6x - 12 = 18

-5x - 12 = 18

-5x = 18+12

-5x = 30

x = 30/(-5)

x = -6

Which is then used to find y

y = 2x+4

y = 2(-6)+4

y = -12+4

y = -8

Put together, the solution is the ordered pair (x,y) = (-6, -8)

--------------------

We can check this through graphing and noting the two lines cross at (-6,-8)

Or we can plug (x,y) = (-6,-8) back into each original equation

Let's do the first equation

x/3 + 2/3 = y/6

-6/3 + 2/3 = -8/6

-6/3 + 2/3 = -4/3

(-6+2)/3 = -4/3

-4/3 = -4/3 ... first equation is confirmed

Now onto the second equation

x/12 - y/4 = 3/2

-6/12 - (-8)/4 = 3/2

-1/2 + 4/2 = 3/2

(-1+4)/2 = 3/2

3/2 = 3/2 .... second equation is confirmed as well

Both equations are true when we plug in (x,y) = (-6, -8) so the answer is confirmed overall.