Answer:
Explanation:
Given:
In this question, I'm asking about the distributive property.
Distributive property is each term within the parentheses can be multiplied by a factor outside the parentheses.
For any real numbers a, b, and c.
Note:
⇒ A(B+C)=AB+AC
⇒ A(B-C)=AB-AC
Solutions:
5(a+2b)-3b
Multiply by expand first.
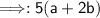
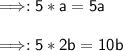
Rewrite the equation problem down.
5a+10b-3b
Solve.
Subtract.
10b-3b=7b

- Therefore, the final answer is 5a+7b.
I hope this helps, let me know if you have any questions.