Question

Find f(x) and g(x) so that the function can be described as y = f(g(x)).

y = 4/x^2+9

Answer 1

f(x) = (4/x)+9 and g(x) = x^2

Explanation:

Answer 2

I'm assuming all of (x^2+9) is in the denominator. If that assumption is correct, then,

One possible answer is
`f(x) = (4)/(x), \ \ g(x) = x^2+9`

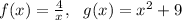
Another possible answer is
`f(x) = (4)/(x+9), \ \ g(x) = x^2`

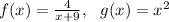
There are many ways to do this. The idea is that when we have f( g(x) ), we basically replace every x in f(x) with g(x)

So in the first example above, we would have

`f(x) = (4)/(x)\\\\f( g(x) ) = (4)/(g(x))\\\\f( g(x) ) = (4)/(x^2+9)`

In that third step, g(x) was replaced with x^2+9 since g(x) = x^2+9.

Similar steps will happen with the second example as well (when g(x) = x^2)