If you meant to write
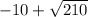 , which is the same as -10+sqrt(210), then the final answer is irrational
, which is the same as -10+sqrt(210), then the final answer is irrational
The value -10 is rational because -10 = -10/1. We can write -10 as a fraction of two integers. We cannot do the same for sqrt(210). The stuff inside (210) is not a perfect square. So sqrt(210) is irrational.
Adding any rational number to an irrational one leads to an irrational number. This is always true. The proof is given below.
----------------------------------------------------------------------------------------
Proof (by contradiction):
Let x be rational and y be irrational.
Since x is rational, this means x = p/q for some integers p,q where q is nonzero.
Assume for a moment that x+y was rational. The goal is to show a contradiction forms. If x+y were rational, then x+y = m/n for some integers m,n with n nonzero.
From here we have the following steps...
x+y = m/n
(p/q) + y = m/n
y = (m/n) - (p/q)
y = (mq)/(nq) - (np)/(nq)
y = (mq - np)/(nq)
y = (some integer)/(some other nonzero integer)
These steps show that y is rational, but this contradicts the definition we set up where y was irrational. The claim "x+y is rational" cannot be the case. The opposite must be true. This concludes that x+y must be irrational.