Question

Wxyz-параллелограмм. Найдите углы угол W, угол X, угол Y и угол Z

Answer 1

∠W = 115°

∠X = 65°

∠Y = 115°

∠Z = 65°

Explanation:

From the picture attached,

Since, sides WX and YZ are parallel and WZ is a transversal,

m∠W + m∠Z = 180° [Sum of consecutive interior angles]

(18b - 11) + (9b + 2) = 180°

27b - 9 = 180°

27b = 189

b =
`(189)/(27)`

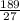
b = 7

m∠W = (18b - 11)° = 115°

m∠Z = (9b + 2)° = 65°

Since, m∠Z = m∠X and m∠W = m∠Y [Property of the angles of a parallelogram]

m∠Z = m∠X = 65°

m∠W = m∠Y = 115°