Answer:
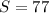
Step-by-step explanation:
So we have the sequence:
1, 2, 3, -4, 1, 2, 3, -4...
This four-number sequence repeats indefinitely.
And we want to find the sum of the first 150 terms.
Note that 150 is equivalent to 148+2.
148 is the same as 4(37).
In other words, our sum is the (1,2, 3, -4) sequence 37 times and then plus the first two numbers of the sequence (1 and 2).
So, our sum is:
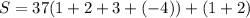
Add:

Multiply:
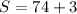
Add:
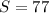
So, our sum is 77.