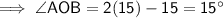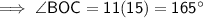1 Answer

LEHO · Answer 1 · 2023-01-29T23:59:23+0000

Answer:

x = 15

∠AOB = 15°

∠BOC = 165°

Explanation:

Angles on a straight line add up to 180°

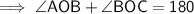
$\sf \implies \angle AOB + \angle BOC=180$

Substitute the given expressions for the angles:

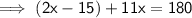
$\sf \implies (2x - 15) + 11x = 180$

Collect and combine like terms:

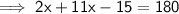
$\sf \implies 2x +11x- 15=180$

$\sf \implies 13x- 15=180$

Add 15 to both sides:

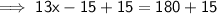
$\sf \implies 13x- 15+15=180+15$

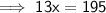
$\sf \implies 13x=195$

Divide both sides by 13:

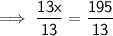
$\sf \implies (13x)/(13)=(195)/(13)$

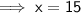
$\sf \implies x=15$

Now substitute the found value of x into the expressions for each angle:

$\sf \implies \angle AOB =2(15)-15=15^(\circ)$

$\sf \implies \angle BOC =11(15)=165^(\circ)$

Please log in or register to add a comment.