Question

If EFH = (5x + 1)°, HFG = 62°, and EFG = (18x + 11)°, find EFH

Answer 1

Given:

Consider the below figure attached with this question.

∠EFH = (5x + 1)°, ∠HFG = 62°, and ∠EFG = (18x + 11)°

To find:

The measure of ∠EFH.

Solution:

From the figure it is clear that ∠EFG is divide in two parts ∠EFH and ∠HFG. So,

`\angle EFG=\angle EFH+\angle HFG`

`18x+11=(5x+1)+(62)`

`18x+11=5x+63`

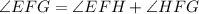
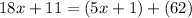
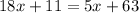
Isolate variable terms.

`18x-5x=63-11`

`13x=52`

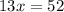
Divide both sides by 13.

`x=(52)/(13)`

`x=4`

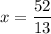
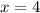
The value of x is 4.

`\angle EFH=(5x+1)^\circ`

`\angle EFH=(5(4)+1)^\circ`

`\angle EFH=(20+1)^\circ`

`\angle EFH=21^\circ`

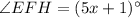
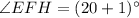
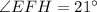
Therefore, the measure of ∠EFH is 21°.