Question

Find the absolute mean deviation for the set {X, 2x, 3x, 4x}

Answer 1

Given:

Data set =
`\{x, 2x, 3x, 4x\}`

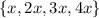
To find:

The absolute mean deviation for the given set.

Solution:

We have,

Data set =
`\{x, 2x, 3x, 4x\}`

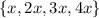
Mean of the data set is

`Mean=(\sum x_i)/(n)`

`Mean=(x+2x+3x+4x)/(4)`

`Mean=(10x)/(4)`

`Mean=2.5x`

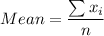
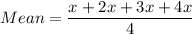
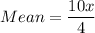
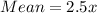
Now,

The formula for mean absolute deviation (MAD) is

`MAD=(\sum |x_i-\overline x|)/(n)`

`MAD=(|x-2.5x|+|2x-2.5x|+|3x-2.5x|+|4x-2.5x|)/(4)`

`MAD=(|-1.5x|+|-0.5x|+|0.5x|+|1.5x|)/(4)`

`MAD=(1.5x+0.5x+0.5x+1.5x)/(4)`

`MAD=(4x)/(4)`

`MAD=x`

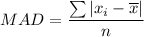
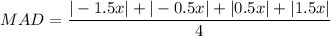
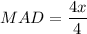
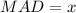
Therefore, the mean absolute deviation for the given set of data is x.