1 Answer

Shabs · Answer 1 · 2021-01-17T05:33:46+0000

Answer:

The inverse is

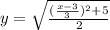
$y =\sqrt{(((x-3)/(3)) ^(2)+5)/(2)}$

Explanation:

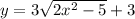
$y=3\sqrt{2x^(2) -5} + 3$

To find the inverse of the function interchange the terms that's x becomes y and y becomes x

We have

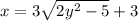
$x=3\sqrt{2y^(2)-5 }+3$

Now solve for y

Move 3 to the other side of the equation

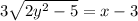
$3\sqrt{2y^(2)-5 } = x-3$

Divide both sides by 3

We have

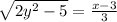
$\sqrt{2y^(2)-5 } =(x-3)/(3)$

square both sides of the equation to remove the square root

That's

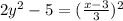
2y^(2)-5 = ((x-3)/(3)) ^(2)

Move 5 to the other side of the equation

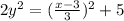
2y^(2) = ((x-3)/(3)) ^(2)+5

Divide both sides by 2

We have

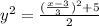
y^(2) = (((x-3)/(3)) ^(2)+5)/(2)

Find the square root of both sides

We have the final answer as

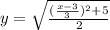
$y =\sqrt{(((x-3)/(3)) ^(2)+5)/(2)}$

Hope this helps you