Problem 6
Answers: Choice A, Choice C, Choice F
Explanation: For each of these answer choices, y goes up as x does as well. Both increase together. As you move from left to right, the graph goes uphill for these intervals. For something like choice B, notice how y drops from y = 50 to y = 40 as x increases, so there's no way to have a positive rate of change. The term "rate of change" is effectively the slope of the straight line through the two points.
=========================================================
Problem 7
I'll do the first two to get you started
For part A, we're looking at the points (-3,0) and (-2,2). Note the x coordinates x = -3 and x = -2
Find the slope of the line through these two points
m = (y2-y1)/(x2-x1)
m = (2-0)/(-2-(-3))
m = 2
Answer to part A is 2
---------------
Same idea, but now we'll use the two points (-2,2) and (1,-4)
m = (y2-y1)/(x2-x1)
m = (-4-2)/(1-(-2))
m = -2
Answer to part B is -2
=========================================================
Problem 8
Answer: The function is positive on two intervals
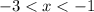 and
and
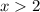
Step-by-step explanation:
We're looking where the curve is above the x axis. The first portion above the x axis is from x = -3 to x = -1, excluding those endpoints (since the endpoints are on the x axis itself). The other portion above the x axis is everything to the right of x = 2
=========================================================
Problem 9
Answer: The function is negative on two intervals
 and
and
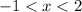
Step-by-step explanation:
Similar to problem 8, but we're now looking below the x axis. The first portion below the x axis is from negative infinity up to x = -3, excluding the endpoints. The other portion is between -1 and 2, excluding those endpoints as well.
=========================================================
Problem 10
Answers: -3, -1, and 2
Step-by-step explanation:
The zeros are also known as the roots or x intercepts. I prefer the term "root" or "x intercept" because the term "zero" might imply that the root has to always be x = 0, but that isn't the case. The x intercept can be anything you want. The graph shows three x intercepts where the curve crosses or touches the x axis. These locations are -3, -1 and 2 on the x axis.
We can say the x intercepts are (-3,0), (-1,0) and (2,0), but that's a bit cumbersome. It's easier to say "roots are -3, -1, and 2".