Given:
Endpoints of a segment are (0,0) and (27,27).
To find:
The points of trisection of the segment.
Solution:
Points of trisection means 2 points between the segment which divide the segment in 3 equal parts.
First point divide the segment in 1:2 and second point divide the segment in 2:1.
Section formula: If a point divides a line segment in m:n, then
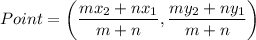
Using section formula, the coordinates of first point are
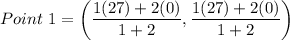
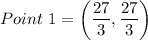
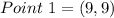
Using section formula, the coordinates of first point are
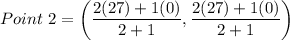

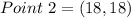
Therefore, the points of trisection of the segment are (9,9) and (18,18).