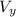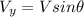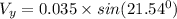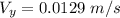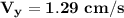Answer:
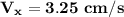
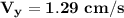
Step-by-step explanation:
Given that:
The radius of the table r = 16 cm = 0.16 m
The angular velocity = 45 rpm
=
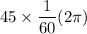
= 4.71 rad/s
However, the relative velocity of the bug with turntable is:
v = 3.5 cm/s = 0.035 m/s
Thus, the time taken to reach the bug to the end is:
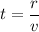
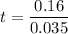
t = 4.571s
So the angle made by the radius r with the horizontal during the time the bug gets to the end is:
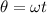
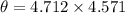
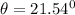
Now, the velocity components of the bug with respect to the table is:
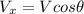
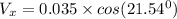
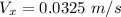

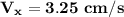
Also, for the vertical component of the velocity