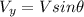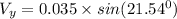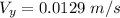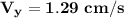Question

A 16-cm-long straight line connects the center of a turntable to its edge. The turntable rotates counter-clockwise at 45 rpm. A bug crawls along the line from the turntable’s center at 3.5 cm s relative to the turntable. Assume it is initially moving in the positive x direction. At the moment the bug gets to the edge, what are the x and y components of the velocity of the bug?

Answer 1

`\mathbf{V_x = 3.25 \ cm/s}`

`\mathbf{V_y = 1.29\ cm/s}`

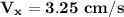
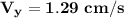
Step-by-step explanation:

Given that:

The radius of the table r = 16 cm = 0.16 m

The angular velocity = 45 rpm

=
`45 * (1)/(60)(2 \pi)`

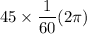
= 4.71 rad/s

However, the relative velocity of the bug with turntable is:

v = 3.5 cm/s = 0.035 m/s

Thus, the time taken to reach the bug to the end is:

`t = (r)/(v)`

`t = (0.16)/(0.035)`

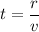
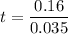
t = 4.571s

So the angle made by the radius r with the horizontal during the time the bug gets to the end is:

`\theta = \omega t`

`\theta = 4.712 * 4.571`

`\theta = 21.54^0`

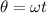
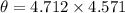
Now, the velocity components of the bug with respect to the table is:

`V_x = Vcos \theta`

`V_x = 0.035 * cos (21.54^0)`

`V_x = 0.0325 \ m/s`

`\text {V_x = 3.25 \ cm/s}`
`\mathbf{V_x = 3.25 \ cm/s}`

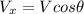
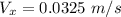
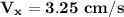
Also, for the vertical component of the velocity
`V_y`

`V_y = V sin \theta`

`V_y = 0.035 * sin (21.54^0)`

`V_y = 0.0129\ m/s`

`\mathbf{V_y = 1.29\ cm/s}`