Full question:
A certain metal crystallizes in a lattice described by a body-centered cubic (bcc) unit cell. The lattice constant (a, the edge of the unit cell) has been measured by X-ray crystallography to be 360 pm. Calculate the radius of an atom of this metal. Be sure your answer has 3 significant digits, and be sure it has the correct unit symbol.
Answer:
r= 156 pm
Step-by-step explanation:
In the body-centered cubic cell, the second layer of spheres fits into the depressions of the first layer and the third layer into the depressions of the second layer (see the first image in the attachment). The coordination number of each sphere in this structure is 8 (each sphere is in contact with four spheres in the layer above and four spheres in the layer below). The coordination number is defined as the number of atoms (or ions) surrounding an atom (or ion) in a crystal lattice.
In the second picture in the attachment we can see that the relationship between the atomic radius r and the edge length a in body-centered cubic cell is:

We are given the value of a, which is 360 pm. What we have to do is to clear r and solve the equation:
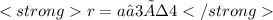
r= 156 pm