Question

Find the absolute maximum and absolute minimum values of f on the given interval. f(t) = 2 cos(t) + sin(2t),[0, π/2].

Answer 1

The absolute maximum is
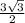`\frac{3\sqrt 3}2` and the absolute minimum value is
`0.`

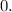
Explanation:

Differentiate of
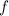`f` both sides w.r.t.
`t`,

`f(t)=2 \cos t+\sin 2t`

`\Rightarrow f'(t)=-2\sin t+2\cos 2t`

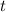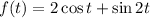
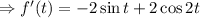
Now take
`f'(t)=0`

`\Rightarrow -2\sin t+2\cos 2t=0`

`\Rightarrow 2\cos 2t=2\sin t`

`\Rightarrow \cos 2t=\sin t`

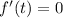
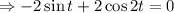
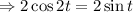
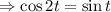
`\Rightarrow 1-2\sin ^2t =\sin t \quad \quad [\because \cos 2t = 1-2\sin ^2t]`

`\Rightarrow 2\sin ^2t+\sin t-1=0`

`\Rightarrow 2\sin ^2t+2\sin t-\sin t-1=0`

`\Rightarrow 2\sin t(\sin t+1)-1(\sin t+1)=0`

`\Rightarrow (\sin t+1)(2\sin t-1)=0`

`\Rightarrow \sin t+1=0 \;\text{and}\; 2\sin t-1=0`

`\Rightarrow \sin t =-1 \;\text{and}\; \sin t =\frac 12`

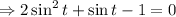
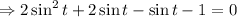
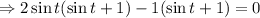
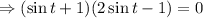
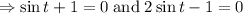
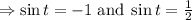
In the interval
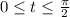`0\leq t\leq \frac {\pi}2`, the answer to this problem is
`\frac {\pi}6`

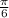
Now find the second derivative of
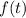`f(t)` w.r.t.
`t`,

`f''(t)=-2\cos t-4\sin 2t`

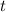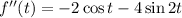
`\Rightarrow \left[f''(t)\right]_{t=\frac {\pi}6}=-2* \frac {\sqrt 3}2-4* \frac{\sqrt 3}2=-3\sqrt 3`

Thus,
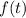`f(t)` is maximum at
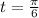`t=\frac {\pi}6` and minimum at
`t=0`

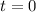
`\left[f(t)\right]_{t=\frac {\pi}6}=2* \frac {\sqrt 3}2+\frac{\sqrt 3}2=\frac{3\sqrt 3}2\;\text{and}\;\left[f(t)\right]_{t=\frac{\pi}2}= 2* 0+0=0`

Hence, the absolute maximum is
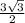`\frac{3\sqrt 3}2` and the absolute minimum value is
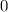`0`.