Question

If tan m=1/2 and tan n=-6 what is the exact value of tan (m+n)

Answer 1

The exact value of tan(m+n) when tan m is 1/2 and tan n is -6 is found to be -1.375 using the tangent sum formula.

Step-by-step explanation:

The exact value of tan (m+n) when tan m=1/2 and tan n=-6 can be found using the tangent sum formula. According to the formula, tan (A+B) = (tan A + tan B) / (1 - tan A * tan B). Plugging in the given values, we get:

tan (m+n) = (tan m + tan n) / (1 - tan m * tan n)

tan (m+n) = (1/2 - 6) / (1 - 1/2 * (-6))

tan (m+n) = (-5.5) / (1 - (-3))

tan (m+n) = (-5.5) / (1 + 3)

tan (m+n) = (-5.5) / 4

tan (m+n) = -1.375

Therefore, the exact value of tan (m+n) is -1.375.

Answer 2

`(-11)/(8)`

Step-by-step explanation:

1) To find tan m = 1/2 on a calculator, you need to take the inverse to find m.

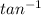`tan^(-1)`(1/2) is about 26°.

So, m = 26°

2) To find tan n = -6 on a calculator, you also need to take the inverse.

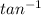`tan^(-1)`(-6) is -80, which is positive 280°. (360° - 80° = 280°)

n = 280°

3) SO, the exact value of tan(m + n) would be tan(26° + 280°), which is tan(306°).

tan(306°) is about -1.376.

The closest answer to -1.376 is the third answer choice, which is -11/8.