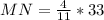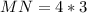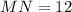Question

HELP ASAP !!!! the points K,L,M and N all lie on the same line segment, in that order, such that the ratio of KL : LM : MN is equal to 4 : 3 : 4. if KN = 33, find MN

Answer 1

`MN = 12`

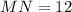
Explanation:

Given that points K, L, M, and N are collinear, and the ratio of the segments, KL:LM:MN = 4:3:4, we can find the lenght of MN as follows, since we are also given the total lenght of the whole segment, KN = 33.

Length of MN = the individual ratio value of MN ÷ the total ratio value of the 3 segments × lenght of the whole segment

Individual ratio value of MN = 4

Total ratio value = 4 + 3 + 4 = 11

Length of whole segment, KN = 33

`MN = (4)/(11)*33`

`MN = 4*3`

`MN = 12`