Question

The intensity of the sunlight that reaches Earth’s upper atmosphere is approximately 1400 W/m2. (a) What is the average energy density? (b) Find the rms values of the electric and magnetic fields. Some useful formulas: I = <> c, <>= 0 Erms2 = Brms2 /0, 0=8.854 x 10-12 C2/(N. m2) , 0= 4  x 10-7 T. m/A, c= 3 x 108 m/s.

Answer 1

(a) Average energy density is 4.67 × 10⁻⁶ J/m³

(b) The rms value of the electric field is 726.26 V/m

and the rms value of the magnetic field 2.42 × 10⁻⁶ T

Step-by-step explanation:

The average energy density < u > is given by

< u > = I / c

Where I is the intensity and

c is the speed of light

From the question

I = 1400 W/m²

c = 3 × 10⁸ m/s

∴ < u > = 1400 W/m² / 3 × 10⁸ m/s

< u > = 4.67 × 10⁻⁶ Ws/m³ (NOTE: Ws = J)

< u > = 4.67 × 10⁻⁶ J/m³

This is the average energy density

(b) From the formula

`< u > = \epsilon _(o) E_(rms) ^(2)`

`E_(rms) = \sqrt{(< u >)/(\epsilon_(o) ) }`

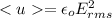
From the question,
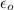`\epsilon _(o)` = 8.854 × 10⁻¹² C²/N.m²

∴
`E_(rms) = \sqrt{(4.67 * 10^(-6) )/( 8.854 * 10^(-12) )`

`E_(rms) = 726.25 V/m`

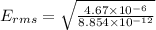
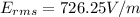
This is the rms value of the electric field

For the rms value of the magnetic field

From

`\epsilon_(o) E_(rms)^(2) = (B_(rms)^(2))/(\mu _(o) )`

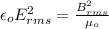
Then,

`{B_(rms) = \sqrt{\mu _(o) \epsilon_(o) E_(rms)^(2)}`

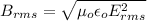
From the question,
`\mu_(o)` = 4π × 10⁻⁷ T.m/A

`{B_(rms) = \sqrt{4\pi * 10^(-7) * 8.854 * 10^(-12) * (726.35)^(2) }`

`{B_(rms) = 2.42 * 10^(-6) T`

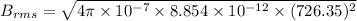
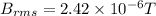
This is the rms value of the magnetic field