Question

Passing through (2, - 2) and perpendicular to the line whose equation is y= 5x+2

Answer 1

Explanation:

Hey there!!!

Here,

Given, A line passes through point (2,-2) and is perpendicular to the y= 5x+2.

The equation of a straight line passing through point is,

`(y - y1) = m1(x - x1)`

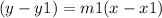
Now, put all values.

`(y + 2) = m1(x - 2)`

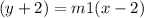
It is the 1st equation.

Another equation is;

y = 5x +2........(2nd equation).

Now, Comparing it with y = mx + c, we get;

m2=5

As per the condition of perpendicular lines,

m1×m2= -1

m1 × 5 = -1

Therefore, m2= -1/5.

Keeping the value of m1 in 1st equation.

`(y + 2) = ( - 1)/(5) (x - 2)`

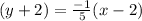
Simplify them.

`5(y + 2) = - x + 2`

`5y + 10 = - x + 2`

`x + 5y + 8 = 0`

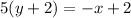
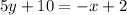
Therefore the required equation is x+5y+8= 0.

Hope it helps...