Answer:
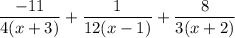
Explanation:
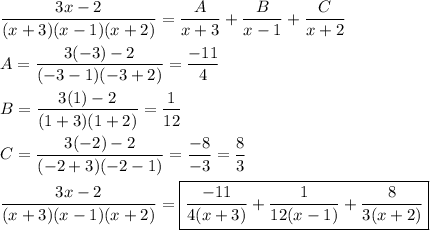
__
When the denominator factors are linear and to the first degree, the corresponding coefficient can be found by eliminating that factor and evaluating the expression for the value of x that would make the factor zero.
As we showed above, the coefficient A is found by evaluating the expression for x=-3 (the zero of the denominator of A) with that factor eliminated from the denominator. Likewise for the others.