Answer:
x =
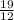 y =
y =
 z =
z =
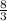 One solution for each variable.
One solution for each variable.
Explanation:
5x + y − z = 6
x + y + z = 2
12x + 4y = 10
The first thing we need to do is solve for x in the 3rd equation because it inly have 2 variables, x and y.
12x + 4y = 10 Subtract 4y from each side
12x + 4y - 4y = 10 - 4y
12x = 10 - 4y Pull 2 out on the right side
12x = 2(5 - 2y) Divide each side by 12
12x/12 = 2(5 - 2y)/12
x = 2(5 - 2y)/12
x = (5 - 2y)/6
Now we plug in our x value into the 2nd equation and solve for z
x + y + z = 2
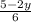 + y + z = 2 Multiply each side by 6
+ y + z = 2 Multiply each side by 6
6(
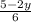 + y + z) = 2 * 6
+ y + z) = 2 * 6
6(
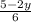 + y + z) = 12
+ y + z) = 12
5 - 2y + 6y + 6z = 12 Combine like terms
5 + 4y + 6z = 12 Subtract 5 from each side
5 - 5 + 4y + 6z = 12 - 5
4y + 6z = 7 Subtract 4y from each side
4y - 4y + 6z = 7 - 4y
6z = 7 - 4y Divide each side by 6
6z/6 = (7 - 4y)/6
z = (7 - 4y)/6
Now we solved for z and x, so in the 1st equation we plug in x and z.
5x + y − z = 6
5(
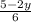 ) + y -
) + y -
 = 6 Multiply each side by 6
= 6 Multiply each side by 6
6*(5(
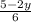 ) ) + 6y - 6(
) ) + 6y - 6(
 ) = 6*6
) = 6*6
6*(5(
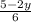 ) ) + 6y - 6(
) ) + 6y - 6(
 ) = 36
) = 36
5(5 - 2y) + 6y - 7 - 4y = 36
25 - 10y + 6y - 7 - 4y = 36 Rearrange to make it easier to combine terms.
25 - 7 - 10y + 6y - 4y = 36
18 - 8y = 36 Subtract 18 from each side.
18 - 18 - 8y = 36 - 18
- 8y = 36 - 18
- 8y = 18 Divide each side by -8
- 8y/-8 = 18/- 8
y = 18/- 8
y = - 9/4
Now we plug our answer for y back into the 3rd equation and solve for the value of x.
12x + 4y = 10
12x + 4
 = 10
= 10
12x - 9 = 10 Add 9 to each side
12x - 9 + 9 = 10 + 9
12x = 10 + 9
12x = 19 Divide each side by 12
12x/12 = 19/12
x = 19/12
Now we have a value for x and y so plug these into the 2nd equation to sovle for z.
x + y + z = 2
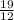 +
+
 + z = 2 We need to find the common denominator in order to add.
+ z = 2 We need to find the common denominator in order to add.
 *
*
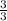 =
=
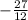
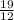
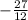 + z = 2
+ z = 2
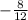 + z = 2 Add
+ z = 2 Add
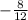 to each side
to each side
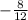
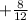 + z = 2
+ z = 2
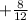
z = 2
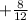 Reduce
Reduce
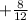 to
to

z = 2 +
 To add find a common denominator.
To add find a common denominator.
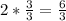
z =
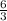 +
+

z =
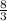
So there is 1 solution for each variable.