Answer:
45 different permutations
Explanation:
Given 10 letters with 8 identical H's and two identical T's, the number of different permutations will be expressed as;
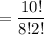
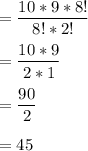
Hence the number of different 10-letter permutations that can be formed from 8 identical H's and two identical T's is 45