Answer:
S₂₀₀ = 121800
Explanation:
the sum to n term of an arithmetic sequence is
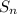 =
=
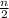 [ 2a₁ + (n - 1)d ]
[ 2a₁ + (n - 1)d ]
where a₁ is the first term and d the common difference
here a₁ = 12 and d = a₂ - a₁ = 18 - 12 = 6 , then
S₂₀₀ =
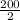 [ (2 × 12) + (199 × 6) ]
[ (2 × 12) + (199 × 6) ]
= 100(24 + 1194)
= 100 ×1218
= 121800