Question

Let x be a random variable representing dividend yield of Australian bank stocks. We may assume that x has a normal distribution with s = 2.3%. A random sample of 11 Australian bank stocks has a mean x = 9.89%. For the entire Australian stock market, the mean dividend yield is μ = 7.9%. Do these data indicate that the dividend yield of all Australian bank stocks is higher than 7.9%? Use a = 0.05. What is the level of significance?

a. 0.025
b. 0.050
c. 0.100
d. 0.900
e. 0.975

Answer 1

a) 0.025 level of significance

The calculated t - value t = 2.88 > 3.58 at 0.025 level of significance

Therefore null hypothesis is rejected

The data indicate that the dividend yield of all Australian bank stocks is higher than 7.9%

Explanation:

Step(i):-

Let 'x' has a normal distribution

Given sample size 'n' =11

Mean of the sample (x⁻) = 9.89% = 0.0989

Standard deviation of the sample (s) = 2.3% = 0.023

Mean of the Population ' μ' = 7.9% = 0.079

Step(ii):-

Null hypothesis:H₀:' μ' = 0.079

Alternative Hypothesis :μ' > 0.079

Test statistic

`t = (x^(-) -mean)/((S)/(√(n) ) )`

`t = (0.0989-0.079)/((0.023)/(√(11) ) )`

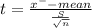
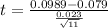
t = 2.8840

Degrees of freedom

ν = n-1 = 11-1 =10

Level of significance

`t_{(\alpha )/(2) } = t_{(0.05)/(2) } = t_(0.025)`

`t_(0.025) , 10 = 3.5814`

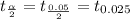
Step(iii):-

The calculated t - value t = 2.88 > 3.58 at 0.025 level of significance

Therefore null hypothesis is rejected

The data indicate that the dividend yield of all Australian bank stocks is higher than 7.9%