Question

The first couple of minutes of the launch of a space shuttle can be described very roughly as follows: The initial mass is 2 x 10 6 kg, the final mass (after 2 minutes) is about 1 x 10 6 kg, the average exhaust speed v ex is about 3000 m/s, and the initial velocity is, of course, zero. If all this were taking place in outer space, with negligible gravity, what would be the shuttle's speed at the end of this stage? What is the thrust during the same period and how does it compare with the initial total weight of the shuttle (on earth)

Answer 1

The shuttle's speed at the end of this stage

`v_s  = 2079.4 \  m/s`

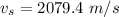
The thrust

`T =  2.5*10^(7) \  N`

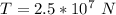
The comparison shows that

`T > W`

Step-by-step explanation:

From the question we are told that

The initial mass is
`m_i = 2*10^(6) \ kg`

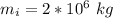
The final mass is
`m_f = 1*10^(6) \ kg`

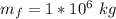
The average speed is
`v = 3000 \ m/s`

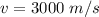
The initial velocity is
`u = 0 \ m/s`

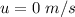
Generally the shuttle's speed at the end of this stage is mathematically represented as

`v_s = v * ln [ (m_i)/(m_f) ]`

=>
`v_s = 3000 * ln [ ( 2*10^(6) )/( 1*10^(6) ) ]`

=>
`v_s = 2079.4 \ m/s`

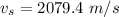
Generally the the initial total weight of the shuttle is mathematically represented as

`W = m_i * g`

=>
`W = 2*10^(6) * 9.8`

=>
`W = 1.96*10^7`

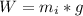
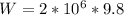
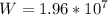
Generally the thrust during the same period is mathematically represented as

`T = v * (m_f)/(m_i)`

=>
`T = 3000 * (1*10^6)/(2*10^(6))`

=>
`T = 2.5*10^(7) \ N`

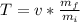
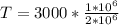
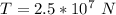
From our calculation we see that

`T > W`