Answer:
t = 3 s and t = 4 s
Explanation:
Given that,
A projectile is fired straight up from ground level with an initial velocity of 112ft/s. Its height as a function of time t is given by :
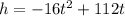
We need to find the interval of time during which the projectile’s height exceeds 192 feet. It means put h = 192 feet
So,
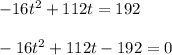
The above is a quadratic equation, it can be solved using middle term splitting as follow :
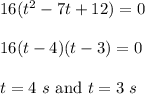
Hence, at t = 3 s and t = 4 s, the projectile’s height exceeds 192 feet above the ground.