Question

A car service chain hopes to increase productivity and has set a goal of an average of at least 25 customers served per day across all their locations. To assess the success of the initiative, the company randomly checks the productivity of 50 locations finding a mean of 24.02 customers served and a standard deviation of 4.75 customers. To find out if there is statistical evidence that the company has failed to meet its goal, answer the following:

Required:
a. Write the appropriate hypotheses.
b. Are the necessary assumptions to perform inference satisfied? Explain.
c. Calculate the p-value.
d. Interpret the p-value you calculated in part (c) within the context of this problem.
e. What is your conclusion?

Answer 1

Explanation:

Given that:

population mean = 25

sample size = 50

sample mean = 24.02

standard deviation = 4.75

The null and alternative hypothesis can be computed as follows:

Null hypothesis:

`\mathbf{H_o : \mu \geq 25}`

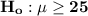
Alternative hypothesis:

`\mathbf{H_1 : \mu < 25}`

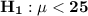
b. Yes, the necessary assumptions to perform the inference are satisfied because the sample size is large and as a result, the data approximately follows a normal distribution.

c. To determine the P-value, we need to Find the t-test statistics which can be expressed by the formula:

`t = (\overline x - \mu)/((\sigma)/(√(n)))`

`t = (24.02 -25)/((4.75)/(√(50)))`

`t = (-0.98)/((4.75)/(7.07))`

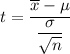
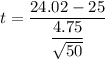
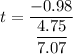
t = - 1.458

The degree of freedom df = n- 1 = 50 - 1 = 49

The p -value = P(T < -1.458)

p -value = 0.0756

d. The p-value is the probability of finding the observed value when null hypothesis is true.

e.

Decision rule: To reject the null hypothesis if the level of significance at 0.05 is greater than the p-value.

Conclusion: We fail to reject the null hypothesis because the p-value is greater than the level of significance, hence, there is no sufficient evidence to conclude that the company has failed to meet its goal.