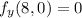Question

Find fx(8, 0) and fy(8, 0) and interpret these numbers as slopes for the following equation.

1. f( x, y) = sqrt(537-x^2-4y^2)
2. fx(8, 0) =
3. fy(8, 0) =
Illustrate with either hand-drawn sketches or computer plots. (Do this on paper. Your instructor may ask you to turn in this work.)

Answer 1

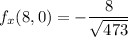`f_x(8,0)= -(8)/( √( 473) )` and
`f_y(8,0)= 0`

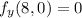
Explanation:

Given that:

`f(x,y) = √(537 -x^2 -4y^2)`

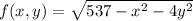
The objective is to determine
`f_x(1,0) \ and \ f_y(1,0)`

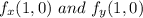
Let determine the partial derivative of the function f with respect to x and y, differentiate partially with respect to x. we have:

`(\partial f(x,y))/(\partial x)=(\partial)/(\partial x ) ( √( 537-x^2-4y^2) )`

`f_x(x,y)= (1)/(2 √( 537-x^2-4y^2) )\ (\partial)/(\partial x ) ( 537-x^2-4y^2 )`

`f_x(x,y)= (1)/(2 √( 537-x^2-4y^2) )\ (-2x)`

`f_x(x,y)= -(x)/( √( 537-x^2-4y^2) )`

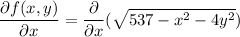
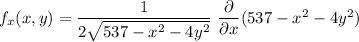
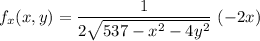
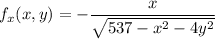
Thus,
`f_x(x,y)= -(x)/( √( 537-x^2-4y^2) )`

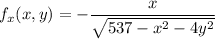
Differentiate partially with respect to y, we have:

`(\partial f(x,y))/(\partial x)=(\partial)/(\partial x ) ( √( 537-x^2-4y^2) )`

`f_y(x,y)= (1)/(2 √( 537-x^2-4y^2) )\ (\partial)/(\partial x ) ( 537-x^2-4y^2 )`

`f_y(x,y)= (1)/(2 √( 537-x^2-4y^2) )\ (-8y)`

`f_y(x,y)= -(4y)/( √( 537-x^2-4y^2) )`

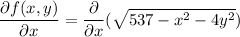
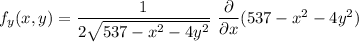
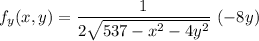
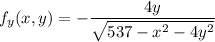
Thus,
`f_y(x,y)= -(4y)/( √( 537-x^2-4y^2) )`

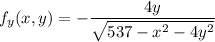
Now, substitute 8 for x and o for y into the function
`f_x(x,y)= -(x)/( √( 537-x^2-4y^2) )`

`f_x(8,0)= -(8)/( √( 537-8^2-4(0)^2) )`

`f_x(8,0)= -(8)/( √( 537-64-0) )`

`f_x(8,0)= -(8)/( √( 473) )`

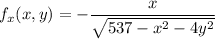
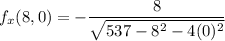
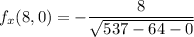
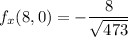
Also, substitute 8 for x and 0 for y into the function
`f_y(x,y)= -(4y)/( √( 537-x^2-4y^2) )`

`f_y(8,0)= -(4(0))/( √( 537-(8)^2-4(0)^2) )`

`f_y(8,0)= -(0)/( √( 537-64-0) )`

`f_y(8,0)= 0`

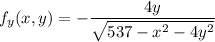
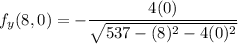
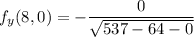
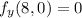
Therefore,
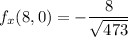`f_x(8,0)= -(8)/( √( 473) )` and
`f_y(8,0)= 0`