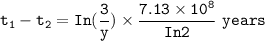Answer:
Step-by-step explanation:
Given that:
The Half-life of
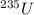 =
=
 is less than that of
is less than that of

Although we are not given any value about the present weight of
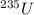 .
.
So, consider the present weight in the percentage of
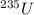 to be y%
to be y%
Then, the time elapsed to get the present weight of
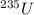 =
=

Therefore;
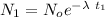
here;
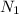 = Number of radioactive atoms relating to the weight of y of
= Number of radioactive atoms relating to the weight of y of
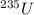
Thus:
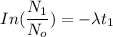
 --- (1)
--- (1)
However, Suppose the time elapsed from the initial stage to arrive at the weight of the percentage of
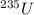 to be =
to be =
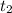
Then:
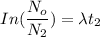 ---- (2)
---- (2)
here;
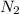 = Number of radioactive atoms of
= Number of radioactive atoms of
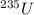 relating to 3.0 a/o weight
relating to 3.0 a/o weight
Now, equating equation (1) and (2) together, we have:
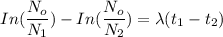
replacing the half-life of
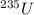 =
=

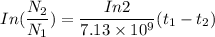 ( since
( since
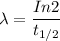 )
)
∴

The time elapsed signifies how long the isotopic abundance of 235U equal to 3.0 a/o
Thus, The time elapsed is