Question

Enter g(x) in terms of f(x) after performing the given transformation of the graph of f(x).

Translate the graph of f(x) to the left 4 units.

Answer 1

Given:

The graph of f(x) translated to the left 4 units.

To find:

The g(x) in terms of f(x) after performing the given transformation of the graph of f(x).

Solution:

The translation is defined as

`g(x)=f(x+a)+b` .... (1)

Where, a is horizontal shift and b is vertical shift.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

Since graph of f(x) translated to the left 4 units, therefore, the value of a is 4 and value of b is 0.

Put a=4 and b=0 in (1).

`g(x)=f(x+4)+0`

`g(x)=f(x+4)`

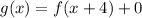
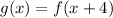
Therefore, the required function is
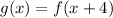`g(x)=f(x+4)`.