Question

Ultraviolet light of wavelength 270 nm strikes a metal whose work function is 2.3 eV.What is the shortest de Broglie wavelength for the electrons that are produced as photoelectrons?

Answer 1

The shortest de Broglie wavelength for the electrons that are produced as photoelectrons is 0.81 nm

Step-by-step explanation:

Given;

wavelength of ultraviolet light, λ = 270 nm

work function of the metal, φ = 2.3 eV = 2.3 x 1.602 x 10⁻¹⁹ J = 3.685 x 10⁻¹⁹ J

The energy of the ultraviolet light is given by;

`E = (hc)/(\lambda)\\\\E = ((6.626*10^(-34) )(3*10^(8)) )/(270*10^(-9) )\\\\E = 7.362 * 10^(-19) \ J`

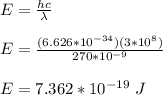
The energy of the incident light is related to kinetic energy of the electron and work function of the metal by the following equation;

E = φ + K.E

K.E = E - φ

K.E = (7.362 x 10⁻¹⁹ J) - (3.685 x 10⁻¹⁹ J )

K.E = 3.677 x 10⁻¹⁹ J

K.E = ¹/₂mv²

mv² = 2K.E

velocity of the electron is given by;

`V = \sqrt{(2K.E)/(m) }\\\\V = \sqrt{(2(3.677*10^(-19)) )/(9.1*10^(-31) ) }\\\\V = 8.99*10^(5) \ m/s`

the shortest de Broglie wavelength for the electrons is given by;

`\lambda = (h)/(mv)\\ \\\lambda = (6.626*10^(-34) )/((9.1*10^(-31))( 8.99*10^(5) ))\\\\\lambda = 8.10*10^(-10) \ m\\\\\lambda = 0.81 \ nm`

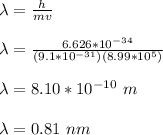
Therefore, the shortest de Broglie wavelength for the electrons that are produced as photoelectrons is 0.81 nm