(a) Each cross section is a square whose side length is decided by the distance in the x,y plane between the two curves
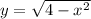 and
and
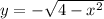 , which is
, which is
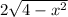 . Then each cross section has area
. Then each cross section has area
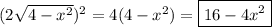
(b) The volume of the solid is obtained by integrating the cross-sectional area from x = -2 to x = 2.
