Question

In how many ways can a set of two nonnegative integers less than 100 be chosen?

Answer 1

Answer: 4950

Explanation:

The number of possible combinations of n things taken r at a time is given by :-

`C(n,r)=(n!)/(r!(n-r)!)`

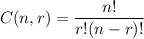
Total nonnegative integers less than 100 ={0,1,2,... ,99} = 100

So, the number of combinations of choosing 2 out of them =
`C(100,2)=(100!)/(2!98!)=(100*99*98!)/(2*98!)\\\\=(100*99)/(2)\\\\=50* 99\\\\=4950`

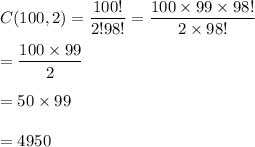
So, the number of ways to choose a set of two nonnegative integers less than 100 = 4950